Funciones

¿Qué es una función?

Una función es la relación entre dos magnitudes, en las que, al menos un valor de estas, llamado dominio, tiene un valor asignado de la otra, llamado imagen.

Para poder representar una función, hace falta saber las siguientes propiedades de esta:

Propiedades de las funciones:

Dominio:

Son los valores de x que tienen una imagen. Pongamos como ejemplo la siguiente función:

y = 2x / x^2 - 4

Simetría:

Una vez sabemos el dominio, necesitamos conocer la simetría de una función. Hay 3 tipos de simetría en las funciones:

• SIMETRÍA PAR 

• SIMETRÍA IMPAR

• SIN SIMETRÍA

Para calcuar la simetría seguimos la siguiente regla:

f(-x) = f(x) --> PAR

f (-x) = -f (x) --> IMPAR

Sigamos con nuestro ejemplo:

Crecimiento:

Puede ser de dos maneras:

• CÓNCAVO --> CRECIMIENTO
• CONVEXO --> DECRECIMIENTO

Asíntotas:

Son las líneas imaginarias a las que la función tiende a acercarse, pero nunca lo logra. Pueden ser de 3 tipos:

• VERTICALES

• HORIZONTALES

• OBLICUAS

Tipos de Funciones:

Rectas:

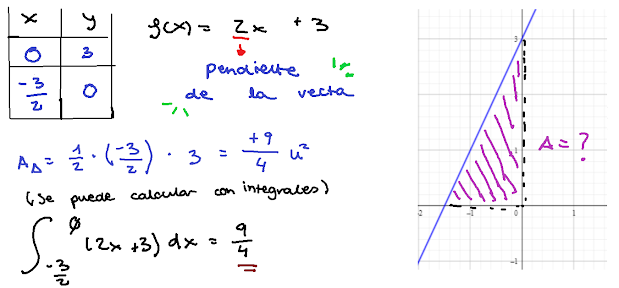
Se trata de funciones que siempre pasan por 2 o más puntos. Para resolverlas, utilizamos una tabla de valores, por ejemplo:

f(x) = 2x + 3

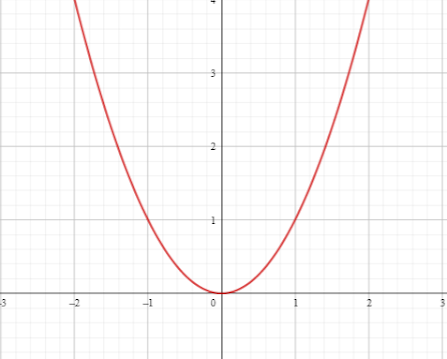
Parábolas:

Una parábola es una función en la que uno de sus términos está elevado al cuadrado. Poseen un vértice, que es cuando la función tiene un rebote. El ejemplo más común es f (x) = x^2:

Existen varias maneras de mover una parábola:

• VERTICALMENTE

• HORIZONTALMENTE